正则化定义为“对学习算法的修改—旨在减少泛化误差而不是训练误差”
- 参数惩罚
对目标函数添加一个参数范数惩罚,用来限制模型的学习能力。
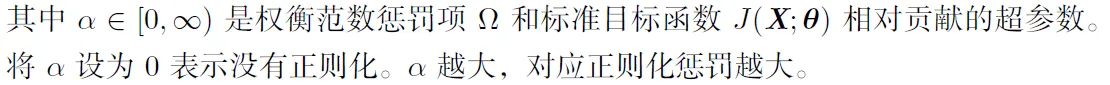
L2权重衰减:
通过添加一个正则项:
使得权重更加接近原点。
现在可以研究正则化后目标函数的梯度,假定没有偏置
通过梯度下降以后可以得到上式子,可以看出每步执行梯度更新前会先收缩权重
上图说明的是沿着特征值较大的方向正则化的影响较小。从几何角度理解:帮助算法往收益最大的方向进行下降,尽量忽视收益小的方向。
L1权重衰减的想法与L2类似:
数据正则化
使机器学习模型效果更好的很自然的一种办法就是给它提供更多的训练数据,当然实际操作中,有时候训练集是有限的,我们可以制造一些假数据并添加入训练集中,当然这仅对某些机器学习问题适用,例如对于图像识别,我们可以平移图像,添加噪声,旋转,色调偏移等等,我们希望模型能够在这些变换或干扰不受影响保持预测的准确性,从而减小泛化误差。当然,我们要注意这些变换不能改变数据的原始标记,如对于识别数字问题,我们就不能对6和9进行180度旋转。
多任务学习
与Dataset augmentation类似,多任务学习也是希望令模型的参数能够进行很好的泛化,其原理是对多个目标共享模型的一部分(输入及某些中间的表示层),使其对于多个有关联的目标均有较好的效果,保证模型可以更好的推广。
提前停止
通常对于较大的模型,我们会观察到训练集上的误差不断减小,但验证集上的误差会在某个点之后反而逐渐增大,这意味着为了减小泛化误差,我们可以在训练过程中不断的记录验证集上的误差及对应的模型参数,最终返回验证集上误差最小所对应的模型参数,这个简单直观的方法就是early stopping,由于其简单高效,在深度学习中得到了广泛应用。
稀疏表示
regularization是使参数更稀疏,同样的我们也可以通过增加对于表征层的norm penalty项使表征(隐藏层)更稀疏。
- Bagging

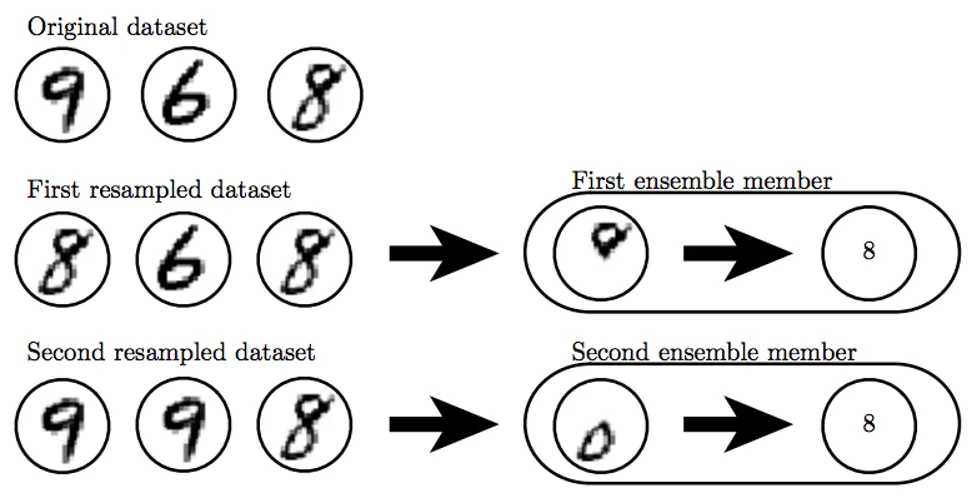
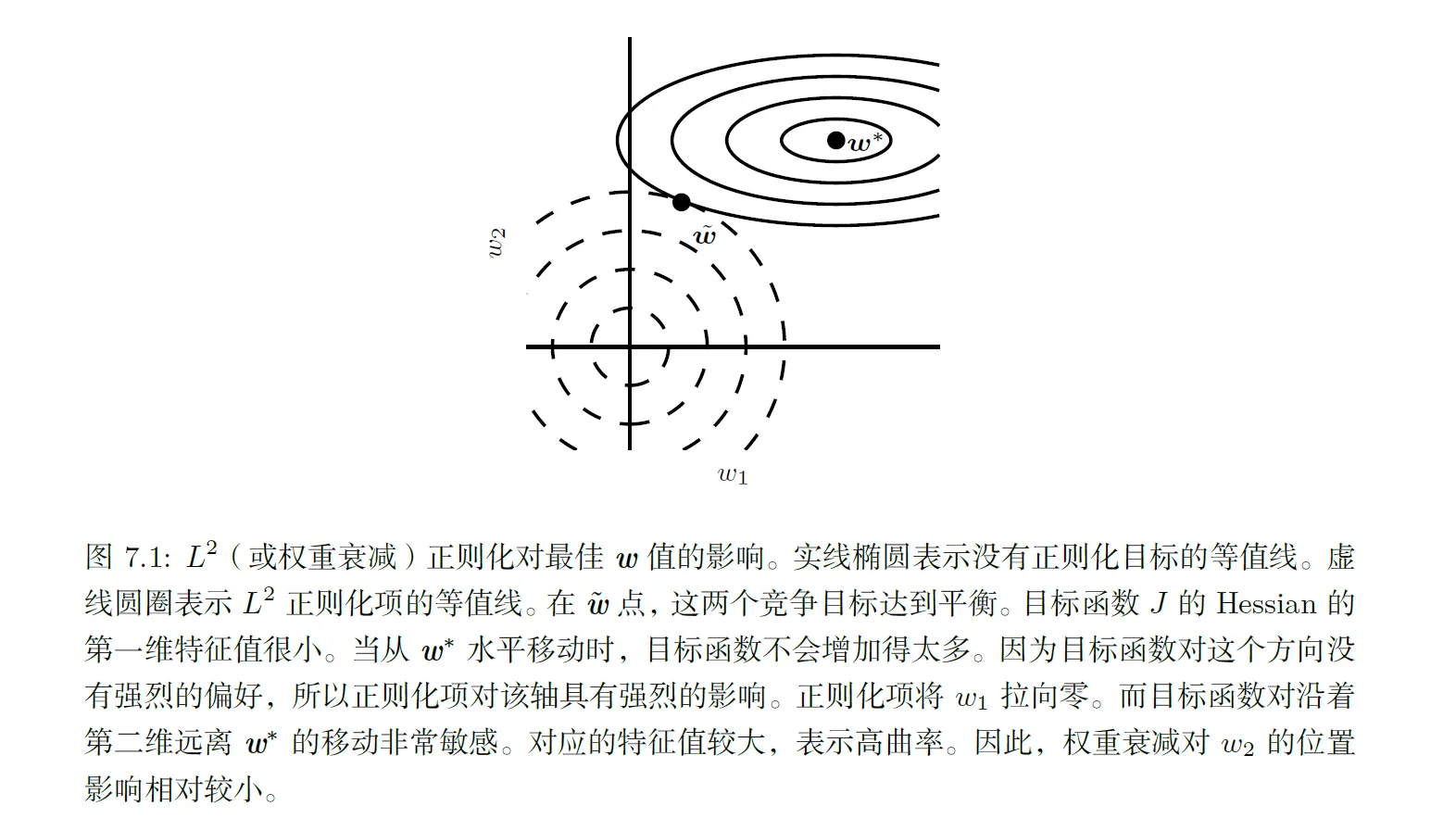
- Dropout可以理解做是将ensemble应用到大型神经网络的一种更为实际有效的方法。由于ensemble需要训练多个模型,对于大型神经网络,其训练和评估所需时间和存储资源较大,这种方法常常不太实际,Dropout就提供了一个更便宜的解决方案:即通过随机去掉一些节点的方法训练多个子网络,并最终将这些子网络ensemble起来,如下图所示:
其具体方法是当我们利用minibatch的算法如随机梯度下降算法来学习时,我们可以随机的选取一个binary mask(0表示节点输出为零,1表示正常输出该节点)决定哪些输入和隐藏层节点保留,每次的mask的选择是独立的。而mask为1的概率是我们可以调控的超参数。
和bagging方法相比,bagging中每个模型是完全独立的,而dropout中,模型间由于继承了父网络中的参数的子集会共享一些参数,这使得在有限的存储空间中我们可以表示多个模型。
以上是训练过程,而在做inference预测时,我们需要取所有模型的预测的均值,但是这往往计算量过多,Hinton提出inference时我们实际可以只用一个模型但其中每个节点的权重需要乘以包含这个节点的概率,这种方法称作weight scaling inference rule。实际中,我们常常把weight scaling过程放在训练过程中,即训练中每个节点输出就乘以包含该节点的概率的倒数,则inference时只需要正常的通过一遍前馈过程即可,不需要在进行weight scaling。
Dropout的优势在于其计算资源占用小,并且对于模型或训练算法的限制较小,基本上可以适用于各种前馈网络,循环网络或概率模型,所以实际工业模型中应用很多。
- 对抗训练
Adversarial Training对抗训练很有意思,它让人们深入思考机器学习究竟学到了什么有效信息。这方面的工作主要是由谷歌的Szegedy和本书作者Ian Goodfellow进行的。他们可以制造一些对抗样本迷惑神经网络,如下图中所示,他们对于熊猫图片加了一些人眼不可见的干扰,形成新样本,而新的人眼仍可鉴定为熊猫的图片却会被机器以较大置信率鉴定为长臂猿。

为什么在人类看来类似的样本机器会得到大相径庭的结论呢?Ian认为这是由于神经网络中的大部分组成还是线性的(如ReLU可以看成是分段线性),而对于不同的输入,线性函数会受到较大的扰动,产生较大的改变。为了解决这一问题,他们会将这些对抗样本重新加到训练集中,使得神经网络倾向于对于数据集保持局部稳定而不至干扰过大,从而学习到更有效的信息。
